学习周报W05

前言

自从上周，我认识到自己的理论远远超过了实践之后，
发觉自己像是个跛脚巨人一般，难以行走。
我需要实践，更多的实践，更好的实践。
所以我尝试更改架构，尝试 <每日一题> 这样的做法。
自此一周，收获颇深。

每日一题

P1518 USACO2.4 两只塔姆沃斯牛 The Tamworth Two

题目描述

两只牛逃跑到了森林里。Farmer John 开始用他的专家技术追捕这两头牛。你的任务是模拟他们的行为（牛和 John）。

追击在 $10 \times 10$ 的平面网格内进行。一个格子可以是：一个障碍物，两头牛（它们总在一起），或者 Farmer John。两头牛和 Farmer John 可以在同一个格子内（当他们相遇时），但是他们都不能进入有障碍的格子。

一个格子可以是：

. 空地；
* 障碍物；
C 两头牛；
F Farmer John。

这里有一个地图的例子：

*...*.....
......*...
...*...*..
..........
...*.F....
*.....*...
...*......
..C......*
...*.*....
.*.*......

牛在地图里以固定的方式游荡。每分钟，它们可以向前移动或是转弯。如果前方无障碍（地图边沿也是障碍），它们会按照原来的方向前进一步。否则它们会用这一分钟顺时针转 90 度。同时，它们不会离开地图。

Farmer John 深知牛的移动方法，他也这么移动。

每次（每分钟）Farmer John 和两头牛的移动是同时的。如果他们在移动的时候穿过对方，但是没有在同一格相遇，我们不认为他们相遇了。当他们在某分钟末在某格子相遇，那么追捕结束。

读入十行表示地图。每行都只包含 10 个字符，表示的含义和上面所说的相同。保证地图中只有一个 F 和一个 C。F 和 C 一开始不会处于同一个格子中。

计算 Farmer John 需要多少分钟来抓住他的牛，假设牛和 Farmer John 一开始的行动方向都是正北（即上）。如果 John 和牛永远不会相遇，输出 0。

输入格式

输入共十行，每行 10 个字符，表示如上文描述的地图。

输出格式

输出一个数字，表示 John 需要多少时间才能抓住牛们。如果 John 无法抓住牛，则输出 0。

输入输出样例 #1

输入 #1

*...*.....
......*...
...*...*..
..........
...*.F....
*.....*...
...*......
..C......*
...*.*....
.*.*......

输出 #1

解题思路

问题的要求有两个：

计算相遇时的分钟数
判断是否进入了死循环

对于 .1 而言，简单模拟即可，然后判断循环开始时是否坐标相同即可。
对于 .2 而言，我们需要记录整个系统（农夫和牛的坐标和朝向）的状态，然后每次循环开始时判断是否进入了相同的状态，从而判断是否进入了循环。

P1067 NOIP 2009 普及组多项式输出

题目描述

一元 $n$ 次多项式可用如下的表达式表示：

$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0,a_n\ne 0$$

其中，$a_ix^i$ 称为 $i$ 次项，$a_i$ 称为 $i$ 次项的系数。给出一个一元多项式各项的次数和系数，请按照如下规定的格式要求输出该多项式：

多项式中自变量为 $x$，从左到右按照次数递减顺序给出多项式。
多项式中只包含系数不为 $0$ 的项。
如果多项式 $n$ 次项系数为正，则多项式开头不出 + 号，如果多项式 $n$ 次项系数为负，则多项式以 - 号开头。
对于不是最高次的项，以 + 号或者 - 号连接此项与前一项，分别表示此项系数为正或者系数为负。紧跟一个正整数，表示此项系数的绝对值（如果一个高于 $0$ 次的项，其系数的绝对值为 $1$，则无需输出 $1$）。如果 $x$ 的指数大于 $1$，则接下来紧跟的指数部分的形式为“$x^b$”，其中 $b$ 为 $x$ 的指数；如果 $x$ 的指数为 $1$，则接下来紧跟的指数部分形式为 $x$；如果 $x$ 的指数为 $0$，则仅需输出系数即可。
多项式中，多项式的开头、结尾不含多余的空格。

输入格式

输入共有 $2$ 行

第一行 $1$ 个整数，$n$，表示一元多项式的次数。

第二行有 $n+1$ 个整数，其中第 $i$ 个整数表示第 $n-i+1$ 次项的系数，每两个整数之间用空格隔开。

输出格式

输出共 $1$ 行，按题目所述格式输出多项式。

输入输出样例 #1

输入 #1

1 2	5 100 -1 1 -3 0 10

输出 #1

1	100x^5-x^4+x^3-3x^2+10

输入输出样例 #2

输入 #2

1 2	3 -50 0 0 1

输出 #2

-50x^3+1

说明/提示

NOIP 2009 普及组第一题

对于100%数据，$0 \le n \le 100$，$-100 \le $系数$ \le 100$

$\text{upd 2022.8.1}$：新增加一组 Hack 数据。

解题思路

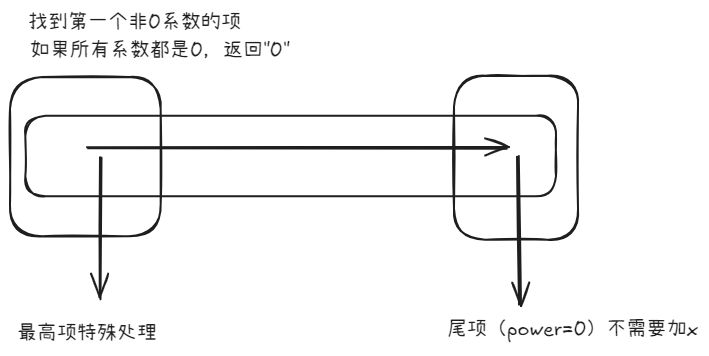
这道题目要求将一元多项式按照特定的格式输出，主要难点在于处理各种特殊情况。解题思路如下：

找到最高次非零项：首先需要找到多项式中次数最高且系数非零的项，因为这个项需要特殊处理（它前面不加”+”号）。
特殊情况处理：
- 当所有系数都为0时，输出”0”
- 对于系数为1的项（非常数项），只输出变量部分，不输出系数
- 对于系数为-1的项（非常数项），只输出”-“加变量部分
- 区分不同指数情况：
  - 指数为0时，只输出系数
  - 指数为1时，输出”x”
  - 指数大于1时，输出”x^n”格式
格式控制：
- 最高次项不带”+”号，如果系数为负，则以”-“开头
- 其他项根据系数正负分别添加”+”或”-“符号
- 系数绝对值为1且非常数项时，不输出”1”
- 保证多项式中只包含系数不为0的项
顺序输出：按照次数递减的顺序输出多项式，不包含系数为0的项。

解决这类问题的关键是考虑全面，确保处理了所有可能的特殊情况，尤其是系数为±1、指数为0/1以及零多项式等边界条件。代码实现时需要仔细区分首项和非首项的处理逻辑，以正确处理符号问题。

P1098 NOIP 2007 提高组字符串的展开

题目描述

在初赛普及组的“阅读程序写结果”的问题中，我们曾给出一个字符串展开的例子：如果在输入的字符串中，含有类似于 d-h 或者 4-8 的字串，我们就把它当作一种简写，输出时，用连续递增的字母或数字串替代其中的减号，即，将上面两个子串分别输出为 defgh 和 45678。在本题中，我们通过增加一些参数的设置，使字符串的展开更为灵活。具体约定如下：

(1) 遇到下面的情况需要做字符串的展开：在输入的字符串中，出现了减号 - ，减号两侧同为小写字母或同为数字，且按照 ASCII 码的顺序，减号右边的字符严格大于左边的字符。

(2) 参数 p1：展开方式。p1=1 时，对于字母子串，填充小写字母；p1=2 时，对于字母子串，填充大写字母。这两种情况下数字子串的填充方式相同。p1=3 时，不论是字母子串还是数字字串，都用与要填充的字母个数相同的星号 * 来填充。

(3) 参数 p2：填充字符的重复个数。p2=k 表示同一个字符要连续填充 k 个。例如，当 p2=3 时，子串d-h 应扩展为 deeefffgggh。减号两边的字符不变。

(4) 参数 p3：是否改为逆序：p3=1 表示维持原来顺序，p3=2 表示采用逆序输出，注意这时候仍然不包括减号两端的字符。例如当 p1=1、p2=2、p3=2 时，子串 d-h 应扩展为 dggffeeh。

(5) 如果减号右边的字符恰好是左边字符的后继，只删除中间的减号，例如：d-e 应输出为 de，3-4 应输出为 34。如果减号右边的字符按照 ASCII 码的顺序小于或等于左边字符，输出时，要保留中间的减号，例如：d-d 应输出为 d-d，3-1 应输出为 3-1。

解题思路

细心题，需要完备的考虑边界情况：

1. 横线连接非法字符，如：

a-1, z-9, a-A, 0-a 要忽略展开，直接输出 -。

2. 两个字符相邻，比如 `a-b`：

r - l == 1，表示中间没有字符可以展开，应该展开为空，不输出 -、也不添加字符。

3. 处理相同字符，如 a-a：

虽然 r >= l，但实际上没有意义，应视为非法，不展开，输出 -。

4. 非法展开：a-a、1-1、c-b（反向）

如果 r <= l，必须 return -。

5. **`p1 == 3`（用 `*` 展开）时忽略大小写**

所有字符都应该是 *。

6. 横线出现在开头或结尾，比如 `-a` 或 `a-`

i - 1 或 i + 1 越界在 main() 中做保护（不进行parse）。

P1591 阶乘数码

题目描述

求 $n!$ 中某个数码出现的次数。

输入格式

第一行为 $t(t \leq 10)$，表示数据组数。接下来 $t$ 行，每行一个正整数 $n(n \leq 1000)$ 和数码 $a$。

输出格式

对于每组数据，输出一个整数，表示 $n!$ 中 $a$ 出现的次数。

解题思路

数组模拟大数，套高精度乘法思路，然后对数组 count 即可。

P1249 最大乘积

题目描述

一个正整数一般可以分为几个互不相同的自然数的和，如 $3=1+2$，$4=1+3$，$5＝1+4=2+3$，$6=1+5＝2+4$。

现在你的任务是将指定的正整数 $n$ 分解成若干个互不相同的自然数（也可以不分解，就是这个数字本身）的和，且使这些自然数的乘积最大。

输入格式

只一个正整数 $n$，（$3 \leq n \leq 10000$）。

输出格式

第一行是分解方案，相邻的数之间用一个空格分开，并且按由小到大的顺序。

第二行是最大的乘积。

解题思路

朴素想法

一开始想到 DFS暴力打表＋找规律：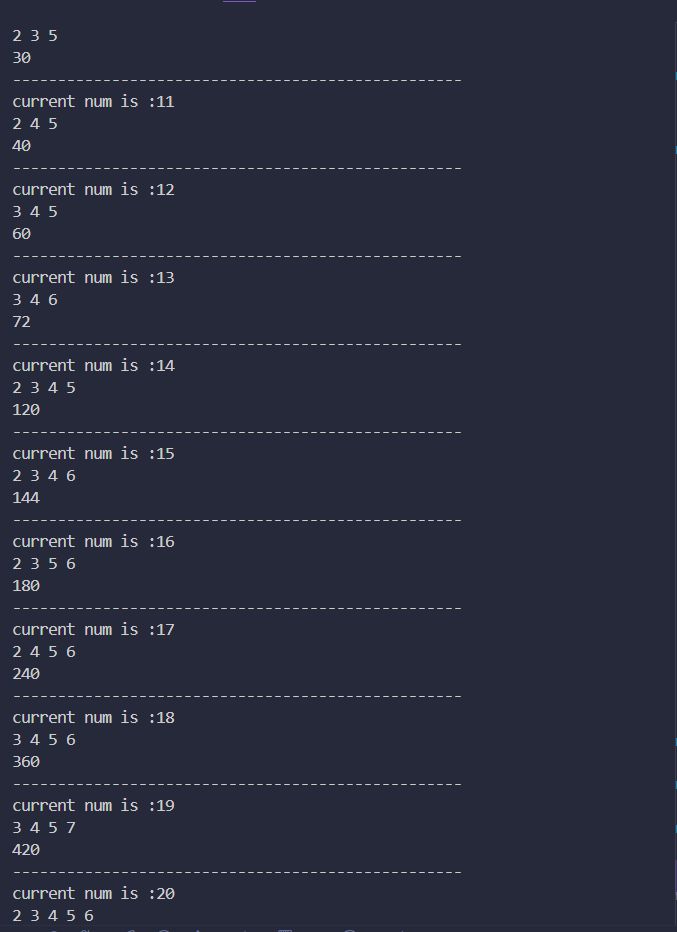

tmd 这谁看的出来有什么规律

迭代一

遂摇 AI 求助

md，看来是我想多了
正解应该就是 dfs + 剪枝了。

剪枝优化的 DFS
我们可以使用 DFS + 回溯来枚举所有递增组合，过程中记录最大乘积方案。

关键点在于：
- 避免重复：每一层从上一次的数字 +1 开始；
- 提前终止：如果当前路径和超过 n，就立即回溯；
- 保存当前最大值和路径。

补兑！TLE 了！
看来正解布什这个。

正解

数学构造 + 贪心优化

不用枚举所有组合，而是直接构造一个乘积最大的“互不相同的自然数和为 n”的序列。

核心思路

目标是：把 n 拆分成互不相同的自然数，使得乘积最大。

这与「均匀拆分」相关。因为在互不相同的前提下，数值越平均，乘积越大。

先打表看看规律：

我们观察到，大部分分解出来的数都是较为连续的。

得出结论

考虑这样一种贪心策略：

首先构造出连续一段自然数，使得和恰好大于或等于 n ，然后找到一个合适的数并更改（如果等于 n 就不更改），使得和满足要求。

例如分解一个数 15 ：

首先找到连续一段自然数序列： (2+3+4+5) <= 15
- 为什么要从 2 开始而不是 3 或更大？因为 1 对乘积没有贡献，但是却占去了 1 的累加和!
发现 2+3+4+5 == 14 ，恰好与 15 相差 1
在序列中找到第一个相加后不重复的数并加上差值（因为构造的序列本身就是有序的）

注意：当 n=3,4 时并不符合上述的贪心策略，需要特判。
时间复杂度：$O(\sqrt{n})$ 构造 + $O(n)$ 乘积计算

P1045 NOIP 2003 普及组麦森数

题目描述

形如 $2^{P}-1$ 的素数称为麦森数，这时 $P$ 一定也是个素数。但反过来不一定，即如果 $P$ 是个素数，$2^{P}-1$ 不一定也是素数。到 1998 年底，人们已找到了 37 个麦森数。最大的一个是 $P=3021377$，它有 909526 位。麦森数有许多重要应用，它与完全数密切相关。

任务：输入 $P(1000<P<3100000)$，计算 $2^{P}-1$ 的位数和最后 $500$ 位数字（用十进制高精度数表示）

输入格式

文件中只包含一个整数 $P(1000<P<3100000)$

输出格式

第一行：十进制高精度数 $2^{P}-1$ 的位数。

第 $2\sim 11$ 行：十进制高精度数 $2^{P}-1$ 的最后 $500$ 位数字。（每行输出 $50$ 位，共输出 $10$ 行，不足 $500$ 位时高位补 $0$）

不必验证 $2^{P}-1$ 与 $P$ 是否为素数。

思路

朴素想法

高精度模板题。
但是需要注意格式输出？
反正我本地的输出是对的，但是提交WA了。
当然，还有TLE了。

第一次勘误

我知道我错哪里了，忘记减一了草。
题目要求输出后500位数字（低到高），我错误理解为前500位（低到高）

结果：过了 50% 的评测点。
其他的都TLE了。
我这个算法是 $O(P^2)$ 的，面对 $P(1000<P<3100000)$ 的规模 TLE 倒也正常。

正解

优化点

二进制快速幂
传统「累乘 2」需要做 $n$ 次乘法，复杂度 $O(n)$；
而二进制快速幂在每一步都把指数右移一位，只做 $O(\log n)$ 次乘法操作，大幅度降低了乘法次数。
同余截断（模 $10^{500}$）
因为题目只关心结果的最低 500 位，我们可以在每一次乘法后就对 $10^{500}$ 取模，把高位「丢弃」，防止大数位数不断膨胀：
这样每次乘法的操作规模都被限制在 500 位之内，空间和时间都可控。
位数计算用对数公式: $\lfloor n\log_{10}2 \rfloor + 1$
能 $O(1)$ 得到 $2^n$ 的十进制位数，而不用先全量计算再测

前言

每日一题

P1518 USACO2.4 两只塔姆沃斯牛 The Tamworth Two

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

解题思路

P1067 NOIP 2009 普及组 多项式输出

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

输入输出样例 #2

输入 #2

输出 #2

说明/提示

解题思路

P1098 NOIP 2007 提高组 字符串的展开

题目描述

解题思路

1. 横线连接非法字符，如：

2. 两个字符相邻，比如 a-b：

3. 处理相同字符，如 a-a：

4. 非法展开：a-a、1-1、c-b（反向）

5. p1 == 3（用 * 展开）时忽略大小写

6. 横线出现在开头或结尾，比如 -a 或 a-

P1591 阶乘数码

题目描述

输入格式

输出格式

解题思路

P1249 最大乘积

题目描述

输入格式

输出格式

解题思路

朴素想法

迭代一

正解

数学构造 + 贪心优化

核心思路

得出结论

P1045 NOIP 2003 普及组 麦森数

题目描述

输入格式

输出格式

思路

朴素想法

第一次勘误

正解

优化点

P1067 NOIP 2009 普及组多项式输出

P1098 NOIP 2007 提高组字符串的展开

2. 两个字符相邻，比如 `a-b`：

5. **`p1 == 3`（用 `*` 展开）时忽略大小写**

6. 横线出现在开头或结尾，比如 `-a` 或 `a-`

P1045 NOIP 2003 普及组麦森数